№ 484 Геометрія = № 39.22 Математика
Доведіть, що сума зовнішніх кутів будь-якого трикутника, взятих по одному при кожній вершині, дорівнює 360°.
Розв'язок:
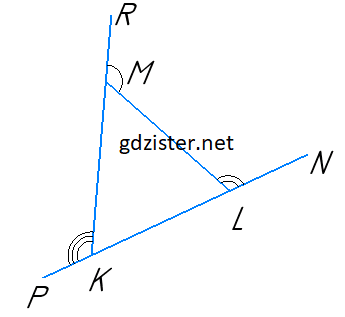
Нехай ΔKNL — даний трикутник.
За властивістю зовнішнього кута трикутника маємо:
∠RML = ∠K + ∠L, ∠MLN = ∠K + ∠M, ∠PKM = ∠M + ∠L.
Додамо рівності:
∠RML + ∠MLN + ∠PKM =
= ∠K + ∠L + ∠K + ∠M + ∠M + ∠L =
= 2(∠K + ∠L + ∠M) = 2 × 180° = 360°. Отже, сума зовнішніх кутів будь - якого трикутника, взятих по одному при кожній вершині, дорівнює 360°.
