№ 482 Геометрія = № 39.20 Математика
Один із зовнішніх кутів рівнобедреного трикутника дорівнює 118°. Знайдіть градусні міри внутрішніх кутів трикутника. Скільки розв’язків має задача?
Розв'язок:
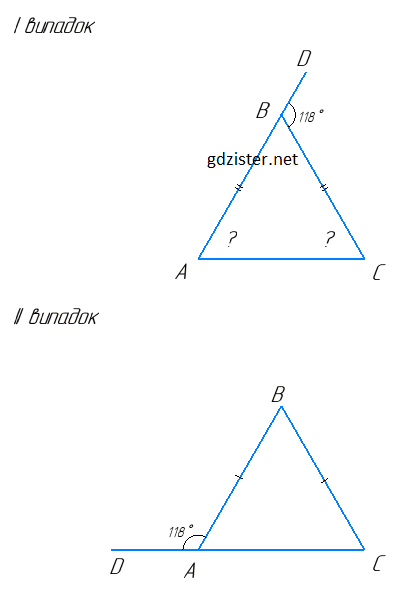
I випадок. Нехай ΔABC — даний рівнобедрений трикутник (AB = BC), ∠A = ∠C. За властивістю зовнішнього кута трикутника:
∠DBC = ∠A + ∠C = 118°,
∠A = ∠C = 118° : 2 = 59°.
∠ABC = 180° – ∠DBC = 180° – 118° = 62°.
II випадок. Нехай ΔABC — даний рівнобедрений трикутник (BA = BC). ∠DAB і ∠BAC — суміжні, їх сума дорівнює 180°.
∠BAC = 180° – 118° = 62°.
Оскільки ∠BAC = ∠BCA (як кути при основі рівнобедреного трикутника), то ∠BCA = 62°.
∠A + ∠B + ∠C = 180°, ∠B =
= 180° – (∠A + ∠C) = 180° – 124° = 56°.
Відповідь:
1) 62°, 59°, 59°.
2) 62°, 62°, 56°.
