№ 481 Геометрія = № 39.19 Математика
Один із зовнішніх кутів трикутника дорівнює 120°. Знайдіть внутрішні кути, які не суміжні з ним, якщо:
1) один з них на 20° менший від другого;
2) один з них утричі менший від другого.
Розв'язок:
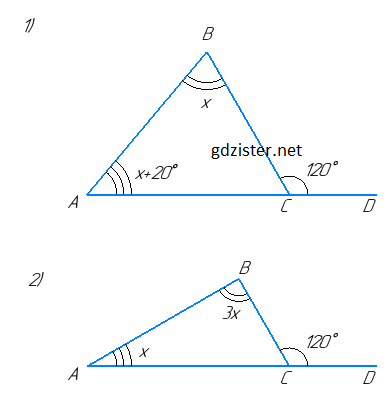
1) Нехай ΔABC — даний трикутник, ∠BCD = 120°, ∠B = x, тоді ∠A = x + 20°.
За властивістю зовнішнього кута трикутника маємо:
∠BCD = ∠A + ∠B.
Складемо рівняння:
x + x + 20° = 120°;
2x = 100°;
x = 50°.
Отже, ∠B = 50°, ∠A = 50° + 20° = 70°.
2) Нехай ΔABC — даний трикутник, ∠A = x, ∠B = 3x.
За властивістю зовнішнього кута трикутника маємо:
∠BCD = ∠A + ∠B.
Складемо рівняння: x + 3x = 120°; 4x = 120°; x = 30°.
Отже, ∠A = 30°, ∠B = 3 × 30° = 90°.
Відповідь:
1) 50°, 70°.
2) 30°, 90°.
