: § 18. Зовнішній кут трикутника та його властивості. Співвідношення між сторонами і кутами трикутника № 463 - 493

Завдання № 479

№ 479 Геометрія = № 39.17 Математика

Зовнішній кут при двох вершинах трикутника відповідно дорівнює 110° і 140°. Знайдіть градусну міру кожного з трьох внутрішніх його кутів.

Розв'язок:

Розв'язок № 479 Геомертія

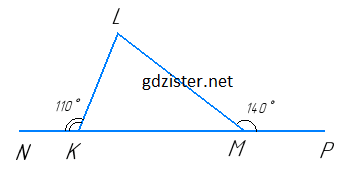
Нехай ΔKLM — даний трикутник, ∠NKL = 110°, ∠LMP = 140°.
∠NKL + ∠LKM = 180° (як суміжні кути).
Звідси ∠LKM = 180° – 110° = 70°.
∠LMP + ∠LMK = 180° (як суміжні кути).
Звідси ∠LMK = 180° – 140° = 40°.
∠L + ∠LKM + ∠LMK = 180° (як сума кутів трикутника).
Звідси ∠L = 180° – (70° + 40°) = 180° – 110° = 70°.

Відповідь:

70°, 70°, 40°.