№ 453 Геометрія = № 38.37 Математика
Доведіть, що бісектриси двох внутрішніх односторонніх кутів при двох паралельних прямих і січній перетинаються під прямим кутом.
Розв'язок:
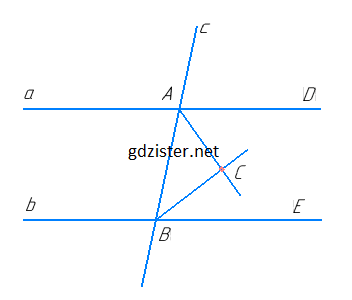
Нехай a∥b, c — січна. ∠DAB і ∠EBA — внутрішні односторонні кути, AC — бісектриса кута DAB, BC — бісектриса кута ABE.
∠DAB + ∠EBA = 180° (за властивістю внутрішніх односторонніх кутів). Оскільки АС — бісектриса ∠DAB, то ∠BAC = $\frac{1}{2}$∠DAB.
Оскільки ВС — бісектриса ∠EBA, то ∠ABC = $\frac{1}{2}$∠EBA.
Отже, ∠BAC + ∠ABC = $\frac{1}{2}$∠DAB + $\frac{1}{2}$∠EBA = $\frac{1}{2}$ (∠DAB + ∠EBA) = $\frac{1}{2}$ × 180° = 90°.
З ΔABC: ∠BAC + ∠ABC + ∠BCA = 180° (за теоремою про суму кутів трикутника).
Звідси ∠BCA = 180° – (∠BAC + ∠ABC) = 180° – 90° = 90°.
Отже, бісектриси двох внутрішніх односторонніх кутів при двох паралельних прямих і січній перетинаються під прямим кутом.
