№ 450 Геометрія = № 38.34 Математика
У трикутнику два кути дорівнюють 70° і 80°. Знайдіть кут між прямими, на яких лежать висоти цих кутів.
Розв'язок:
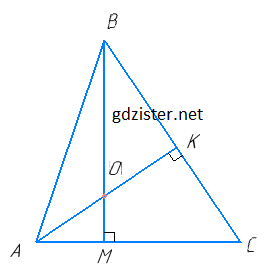
Нехай у ΔABC ∠A = 70°, ∠B = 80°. BM ⊥ AC, AK ⊥ BC.
У ΔABM: ∠A = 70°, ∠BMA = 90° (оскільки BM — висота).
∠A + ∠ABM + ∠BMA = 180° (за теоремою про суму кутів трикутника). Звідси ∠ABM = 180° – (∠A + ∠BMA) = 180° – (40° + 90°) = 180° – 160° = 20°.
З ΔABK: ∠B = 80°, ∠AKB = 90° (оскільки AK ⊥ BC).
За теоремою про суму кутів трикутника маємо: ∠BAK + ∠B + ∠AKB = 180°.
Звідси ∠BAK = 180° – (∠B + ∠AKB) = 180° – (80° + 90°) = 180° – 170° = 10°.
Розглянемо ΔAOB. ∠BAK + ∠ABM + ∠BOA = 180°.
Звідси ∠BOA = 180° – (∠BAK + ∠ABM) = 180° – (10° + 20°) = 180° – 30° = 150°.
Оскільки кут між прямими не перевищує 90°, то кутом між прямими, яким належать висоти, буде кут суміжний з кутом BOA, це кут ∠AOM = 180° – 150° = 30°.
Відповідь:
30°.
