Завдання № 448

№ 448 Геометрія = № 38.32 Математика

Умова:

Доведіть рівність трикутників ABC і A₁B₁C₁, якщо BC = B₁C₁, ∠A = ∠A₁, ∠B = ∠B₁. 

Розв'язок:

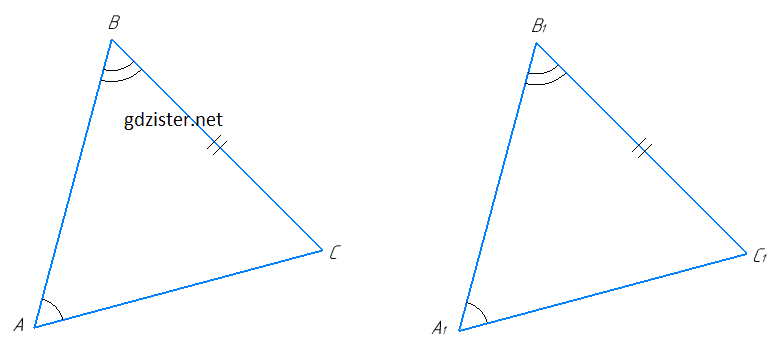
BC = B₁C₁, ∠A = ∠A₁, ∠B = ∠B₁.
У ΔABC: ∠C = 180° – (∠A + ∠B).
У ΔA₁B₁C₁: ∠C₁ = 180° – (∠A₁ + ∠B₁).
Оскільки ∠A = ∠A₁ і ∠B = ∠B₁, то ∠C = ∠C₁.
Отже, ΔABC = ΔA₁B₁C₁ за другою ознакою рівності трикутників (BC = B₁C₁, ∠B = ∠B₁ – за умовою, ∠C = ∠C₁ – за розв'язанням).

Відповідь: