№ 407 Геометрія = № 31.9 Математика
Дано: АО = ОВ, СО = OD. Довести: ∆АВС = ∆BAD.
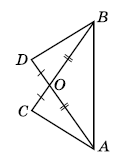
Розв'язок:
AO = OB, CO = OD за умовою.
∠DOB = ∠COA — як вертикальні кути.
Отже, ΔDOB = ΔCOA за першою ознакою рівності трикутників. У рівних трикутників відповідні сторони рівні, тому DB = CA. DA = DO + OA, CB = CO + OB, DA = CB, оскільки DO = CO, OA = OB. AB — спільна сторона ΔABC і ΔBAD.
Отже, ΔABC = ΔBAD за третьою ознакою рівності трикутників.
