№ 404 Геометрія = № 31.6 Математика
На малюнку АВ = ВС, АК = КС. Доведіть, що BK - бісектриса кута ABC.
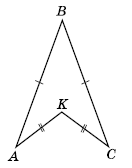
Розв'язок:
З'єднуємо точку В і точку С. Отримаємо два трикутники: ΔABK і ΔCBK.
AB = BC, AK = KC за умовою, BK — спільна сторона ΔABK і ΔCBK.
Отже, ці трикутники рівні за третьою ознакою рівності трикутників.
У рівних трикутників відповідні кути рівні, тому ∠ABK = ∠CBK.
Отже, BK — бісектриса кута ABC.
