№ 393 Геометрія = № 30.22 Математика
Доведіть. що коли медіана трикутника є його бісектрисою, то трикутник - рівнобедрений.
Розв'язок:
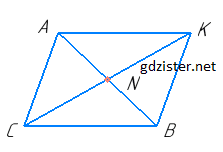
Нехай в ΔABC CN – медіана і бісектриса.
Продовжимо медіану CN так, щоб NK = CN. Проведемо відрізки КА і КВ.
Розглянемо ΔCNB і ΔKNA. CN = KN (за побудовою), NB = NA (за умовою). ∠ANK = ∠BNC (як вертикальні), отже, ΔCNB = ΔKNA за двома сторонами і кутом між ними. У рівних трикутників рівні відповідні кути і сторони, тож ∠NCB = ∠NKA, CB = KA.
Аналогічно з рівності трикутників CAN і KBN отримаємо ∠CAN = ∠BKN, AC = BK. Розглянемо ΔCAN і ΔKBС. Вони рівнобедрені. AK = CA, CB = BK.
Отже, отримали AC = CB = AK = KB. У ΔABC дві сторони рівні, він рівнобедрений.0
