№ 390 Геометрія = № 30.19 Математика
Доведіть. що в рівнобедреному трикутнику бісектриси. про ведені до бічних сторін. - рівні.
Розв'язок:
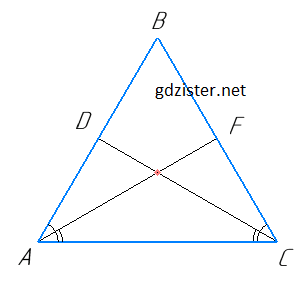
Нехай в ΔABC AB = BC, ∠BAC = ∠BCA, AF і CD — бісектриси,
тобто ∠FAC = ∠FAB = ∠BAC, ∠DCA = ∠DCB = ∠BCA, отже, ∠FAC = ∠DCA, ΔADC = ΔCFA (оскільки AC — спільна, ∠FAC = ∠DCA, ∠DAC = ∠FCA).
З рівності трикутників маємо: AF = CD.
