№ 389 Геометрія = № 30.18 Математика
Доведіть, що в рівнобедреному трикутнику медіани, проведені до бічних сторін, - рівні.
Розв'язок:
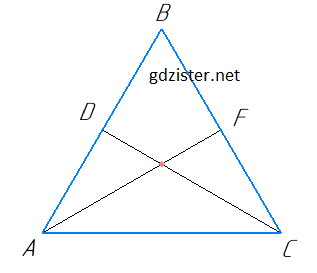
Нехай в ΔABC AB = BC, BF = FC = BC, BD = DA = AB, отже, AD = FC.
ΔADC = ΔCFA (оскільки AC — спільна, ∠DAC = ∠FCA — як кути при основі рівнобедреного трикутника, AD = FC — як половини рівних сторін AB і BC).
З рівності трикутників маємо: DC = FA.
