Завдання № 388

№ 388 Геометрія = № 30.17 Математика

AD і A₁D₁ -  відповідно бісектриси рівних трикутників АВС і А₁В₁С₁. Доведіть, що ∆АDС = ∆А₁D₁С₁.

Розв'язок:

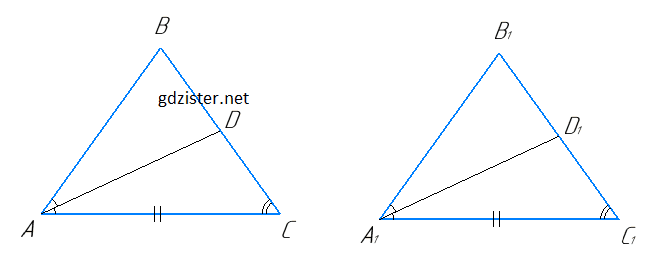
ΔABC = ΔA₁B₁C₁, отже,
A₁C₁ = AC, ∠B₁C₁A₁ = ∠BCA (як відповідні сторони і кути рівних трикутників).
AD — бісектриса ΔABC, ∠BAD = ∠DAC. A₁D₁ — бісектриса ΔA₁B₁C₁,
∠B₁A₁D₁ = ∠D₁A₁C₁. Отже, ∠DAC = ∠D₁A₁C₁.
ΔADC = ΔA₁D₁C₁ — за стороною і прилеглими кутами.