№ 368 Геометрія = № 29.25 Математика
Відрізки АС і BD перетинаються в точці О так, що ∆АОВ = ∆COD. Точка К належить відрізку АВ, а точка L - відрізку DC, причому KL проходить через точку О. Доведіть, що КО = OL і КВ = DL.
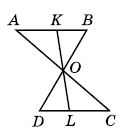
Розв'язок:
Оскільки ΔAOB і ΔCOD рівні, то рівні їхні відповідні кути і сторони, тобто ВО = OD, ∠ABO = ∠CDO.
Розглянемо ΔKBO і ΔLDO.
∠KOB = ∠LOD — як вертикальні кути.
ΔKBO = ΔLDO за стороною і прилеглими кутами.
Отже, KO = OL, KB = DL.
