№ 364 Геометрія = № 29.21 Математика
На бічних сторонах АВ і ВС рівнобедреного трикутника АВС позначено точки К і L так, що ∠КСА = ∠LAC. Доведіть, що відрізки АК і CL рівні.
Розв'язок:
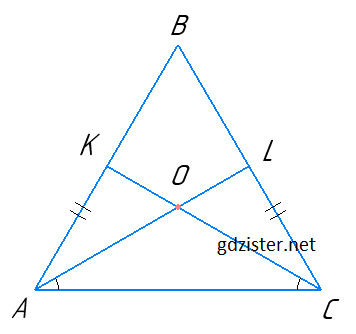
Нехай ΔABC — рівнобедрений, AB = BC, ∠KCA = ∠LAC.
Розглянемо ΔAOC.
Оскільки ∠KCA = ∠LAC, то за теоремою 2 ΔAOC — рівнобедрений.
Звідси OA = OC.
Розглянемо ΔKOA і ΔLOC. ∠KAO = ∠BAC - ∠LAC, ∠LCO = ∠BCA - ∠KCA.
Оскільки ∠BAC = ∠BCA і ∠KCA = ∠LAC, то ∠KAO = ∠LCO.
∠KOA = ∠LOC — як вертикальні.
Отже, ΔKOA = ΔLOC за стороною і прилеглими кутами.
Звідси AK = CL.
