№ 363 Геометрія = № 29.20 Математика
На бічних сторонах АВ і ВС рівнобедреного трикутника АВС позначено точки К і L так, що АК = LC. Доведіть, що AL = КС.
Розв'язок:
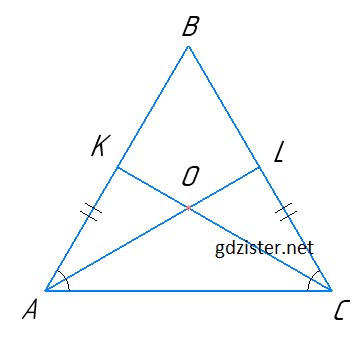
Оскільки ΔABC — рівнобедрений (AB = BC) з основою AC, то ∠BAC = ∠BCA (за властивістю кутів рівнобедреного трикутника).
Розглянемо ΔCKA і ΔALC: AC — спільна, KA = LC (за умовою), ∠KAC = ∠LCA.
Отже, ΔCKA = ΔALC (за двома сторонами і кутом між ними).
Отже, AL = KC (як відповідні сторони).
