№ 337 Геометрія = № 28.19 Математика
Умова:
∆АКС = ∆ALC. Доведіть, що ∆ВКС = ∆BLC.
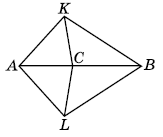
Розв'язок:
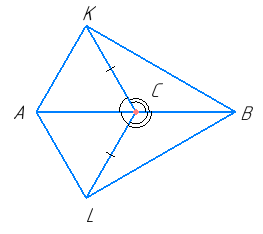
Оскільки ΔAKC = ΔALC, то у них відповідні сторони і кути рівні.
Отже, KC = LC, ∠KCA = ∠LCA. Оскільки ∠KCA = ∠LCA, то рівні і суміжні з ними кути ∠KCB = ∠LCB. CB — спільна сторона трикутників ВКС і BLC.
Отже, ΔBKC = ΔBLC за двома сторонами і кутом між ними.