№ 338 Геометрія = № 28.20 Математика
На бісектрисі кута А позначили точку В, а на його сторонах такі точки М і N, що ∠ABM = ∠ABN. Доведіть, що MN ⟂ АВ.
Розв'язок:
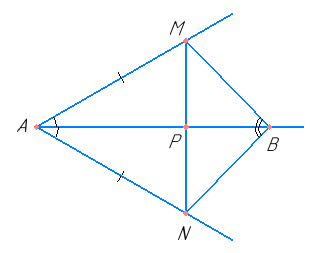
Оскільки AB — бісектриса кута A, то ∠MAB = ∠NAB, AB — спільна сторона трикутників AMB і ANB.
Отже, ΔAMB = ΔANB за стороною і прилеглими кутами.
У рівних трикутників відповідні сторони рівні. Отже, AM = AN.
Розглянемо ΔAMP і ΔANP. AP — спільна сторона.
ΔAMP = ΔANP за двома сторонами і кутом між ними (∠MAP = ∠NAP, AM = AN).
У рівних трикутників відповідні кути рівні, отже, ∠MPA = ∠NPA.
Оскільки ці кути суміжні і рівні, то маємо ∠MPA + ∠NPA = 180°; ∠MPA = ∠NPA = 90°.
Тож MN ⊥ AB.
