№ 336 Геометрія = № 28.18 Математика
Умова:
∆АВК= ∆CBL. Доведіть, що ∆ABL = ∆СВК.
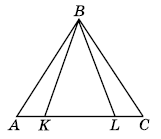
Розв'язок:
Оскільки ΔABK = ΔCBL, то у них відповідні сторони і кути рівні.
Отже, ∠A = ∠C, AB = CB, AK = CL.
AL = AK + KL, CK = CL + KL, отже, KL — спільний відрізок для AL і CK, AL = CK.
Тоді ΔABL = ΔCBK за двома сторонами і кутом між ними.