№ 279 Геометрія = № 22 ВПТ 4 Математика
Один з внутрішніх односторонніх кутів, що утворилися при перетині паралельних прямих січною, дорівнює 72°. Знайдіть кут між бісектрисами внутрішніх односторонніх кутів.
Розв'язок:
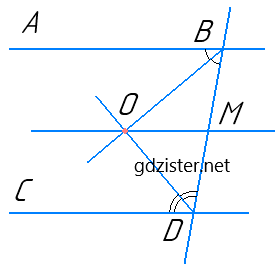
Нехай паралельні прямі AB і CD перетинає пряма BD;
∠ABD і ∠CDB — внутрішні односторонні кути;
∠ABD = 72°, тоді ∠CBD = 180° - ∠ABD, ∠CDB = 180° - 72° = 108°;
BO — бісектриса ∠ABD, DO — бісектриса ∠CDB, тоді
∠ABO = $\frac{1}{2}$ ∠ABD = $\frac{1}{2}$ × 72° = 36°;
∠CDO = $\frac{1}{2}$ ∠CDB = $\frac{1}{2}$ × 108° = 54°.
Проведемо через точку O пряму OM ∥ CD, тоді OM ∥ AB.
∠BOM = ∠ABO = 36°; ∠DOM = ∠CDO = 54°.
∠BOD — кут між бісектрисами внутрішніх односторонніх кутів, ∠BOD = ∠BOM + ∠DOM; ∠BOD = 36° + 54° = 90°.
Відповідь:
90°.
