№ 280 Геометрія = № 23 ВПТ 4 Математика
Прямі АВ і CD паралельні. Знайдіть ∠MNB.
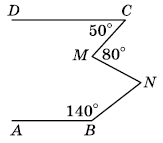
Розв'язок:
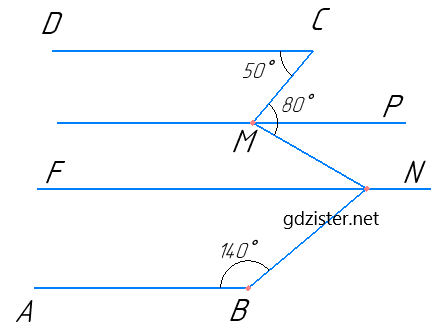
Проведемо пряму MP ∥ DC і пряму NF ∥ BA. ∠MNB = ∠MNF + ∠FNB.
Розглянемо DC ∥ MP і січну CM: ∠CMP = ∠DCM = 50° — як внутрішні різносторонні кути. ∠PMN = ∠CMN - ∠CMP = 80° - 50° = 30°.
Розглянемо MP ∥ NF і січну MN: ∠MNF = ∠PMN = 30° — як внутрішні різносторонні кути.
Розглянемо NF ∥ AB і січну NB: ∠FNB + ∠ABN = 180° — як внутрішні односторонні кути.
∠FNB = 180° - 140° = 40°. Отже, ∠MNB = 30° + 40° = 70°.
Відповідь:
70°.
