№ 256 Геометрія = № 35 ВПТ 2 Математика
Знайдіть градусну міру кожного із чотирьох кутів, що утворилися при перетині двох прямих, якщо сума двох із цих кутів:
1) менша від суми двох інших у 4 рази;
2) більша за суму двох інших на 160°.
Розв'язок:
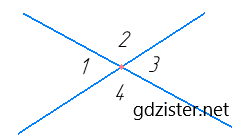
1) Нехай ∠1 = x, ∠3 = ∠1 = x (як вертикальні кути).
∠2 + ∠4 = 4(∠1 + ∠3) = 2 × 4x = 8x.
Сума всіх утворених кутів дорівнює 360°.
2x + 8x = 360°
10x = 360°
x = 36°
Отже, ∠1 = ∠3 = 36°, ∠2 = ∠4 = 180° - 36° = 144°.
2) Нехай ∠1 = x, ∠3 = ∠1 = x (як вертикальні кути).
∠1 + ∠3 = x + x = 2x.
∠2 + ∠4 = 4(∠1 + ∠3) = 2x + 160°.
Сума всіх утворених кутів дорівнює 360°.
2x + 2x + 160° = 360°
4x = 200°
x = 50°
Отже, ∠2 = 180° - 50° = 130°.
Відповідь:
1) 36°, 36°, 144°, 144°.
2) 50°, 50°, 130°, 130°.
