ДСР 2 Геометрія = ДСР 4 Математика
Промінь ОС проходить між сторонами кута АОВ. ОК - бісектриса кута АОС, OL - бісектриса кута СОВ. ОК ⊥ OL. Визначте вид кута АОВ.
А. гострий
Б. тупий
В. прямий
Г. розгорнутий
Розв'язок:
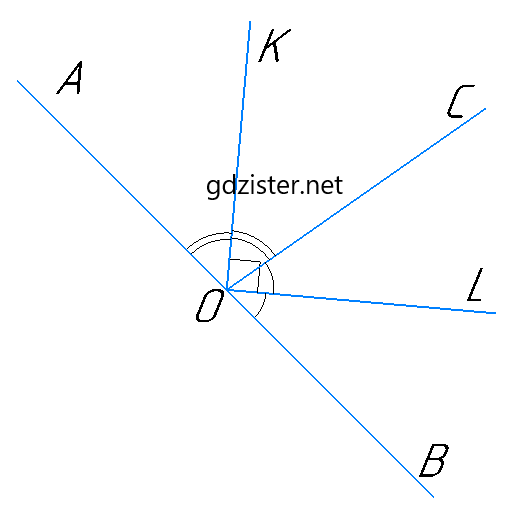
Оскільки OK — бісектриса ∠AOC, цей кут розділяється на дві рівні частини: ∠AOK та ∠KOC.
∠AOC = ∠AOK + ∠KOC = 2∠KOC
Оскільки OL — бісектриса ∠COB, цей кут розділяється на дві рівні частини: ∠COL та ∠LOB.
∠COB = ∠COL + ∠LOB = 2∠COL
За умовою, OK перпендикулярний до OL, тобто кут між ними, ∠KOL, дорівнює 90°.
Оскільки ∠AOC складається з кутів AOK і KOC, а ∠COB складається з кутів COL і LOB, то:
∠AOB = ∠AOC + ∠COB = 2∠KOC + 2∠COL = 2(∠KOC + ∠COL) = 2∠KOL = 2 × 90° = 180°.
Відповідь:
Г. розгорнутий
