№ 157 Геометрія = № 16.20 Математика
Доведіть, що промінь, проведений через вершину кута перпендикулярно до його бісектриси, є бісектрисою кута, суміжного з даним.
Розв'язок:
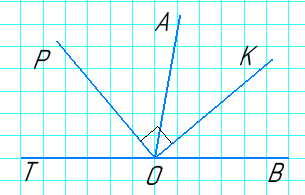
Нехай ∠АОВ – заданий кут, ОК – бісектриса кута АОВ. РО ⊥ ОК, отже, ∠РОК = 90°.
∠ТОВ – розгорнутий кут, ∠ТОВ = 180°.
∠ТОВ = ∠ТОР + ∠РОА + ∠АОК + ∠КОВ = 180°.
Оскільки ∠РОК = 90°, то ∠РОА + ∠АОК = 90°, ∠ТОР + 90° + ∠КОВ = 180°, звідси ∠ТОР + ∠КОВ = 90°.
Якщо ∠КОВ = ∠АОК, то ∠ТОР = ∠РОА.
Отже, ОР – бісектриса кута ТОА.