№ 156 Геометрія = № 16.19 Математика
Умова:
На малюнку ∠AOB = ∠COD, ∠BOC = ∠DOE. Доведіть, що ОС ⟂ АЕ і ВО ⟂ OD.
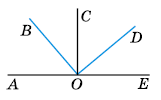
Розв'язок:
1) Позначимо ∠AOB = ∠COD = x; ∠BOC = ∠DOE = y.
Оскільки ∠АОВ + ∠BOC + ∠COD + ∠DOE = 180°, то 2х + 2у = 180°; 2(х + у) = 180°; х + у = 90°.
2) ∠АОС = ∠АОВ + ∠ВОС = х + у = 90°, тому ОС ⊥АЕ.
3) ∠BOD = ∠BOC + ∠COD = х + у = 90°, тому ВО ⊥ OD.
Задачу доведено.