№ 235 Геометрія = № 19.24 Математика
Доведіть, що бісектриси пари внутрішніх різносторонніх кутів, утворених при перетині двох паралельних прямих січною, паралельні.
Розв'язок:
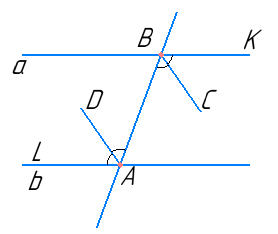
Оскільки a ∥ b, то ∠KBA = ∠BAL (як внутрішні різносторонні).
Оскільки BC і AD — бісектриси цих кутів, то ∠CBA = ∠DAB (як половини рівних кутів).
Розглянемо прямі BC і AD та січну AB. ∠CBA і ∠DAB — внутрішні різносторонні рівні, отже, BC ∥ DA.
Отже, бісектриси двох внутрішніх різносторонніх кутів при паралельних прямих і січній паралельні.
