№ 236 Геометрія = № 19.25 Математика
Доведіть, що бісектриси пари відповідних кутів, утворених при перетині двох паралельних прямих січною, паралельні.
Розв'язок:
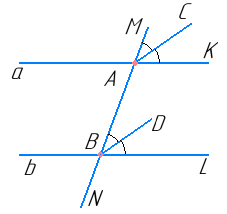
Оскільки a ∥ b, то ∠MAK = ∠ABL (як відповідні кути).
Оскільки AC і BD — бісектриси цих кутів, то ∠ABD = ∠MAC (як половини рівних кутів).
Розглянемо прямі AC і BD і січну MN: ∠MAC і ∠ABD — відповідні кути і рівні. Отже, AC ∥ BD.
Отже, бісектриси двох відповідних кутів при паралельних прямих і січній паралельні.
