№ 59 Геометрія = № 6.21 Математика
Кут між бісектрисою кута і продовженням однієї з його сторін за вершину кута дорівнює 142°. Знайдіть градусну міру цього кута.
Розв'язок:
Нехай АОС – заданий кут. ОМ – продовження сторони ОА з вершиної О.
ОК – бісектриса кута АОС. ∠АОМ – розгорнутий, ∠АОМ = 180°.
∠КОМ = 142°, ∠АОМ = ∠АОК + ∠КОМ.
Отже, ∠АОК = 180° - 142° = 38°.
Оскільки ОК – бісектриса кута АОС, то ∠КОС = ∠АОК = 38°.
Тоді ∠АОС = ∠АОК + ∠КОС = 38° + 38° = 76°.
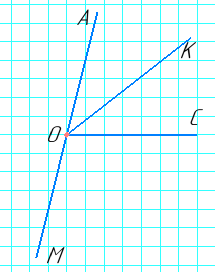
Відповідь:
∠АОС = 76°.
