№ 32 ДТ Геометрія = № 32 ДТ Математика
Побудуйте трикутник за радіусом описаного кола, стороною та висотою, що проведена до цієї сторони.
Розв'язок:
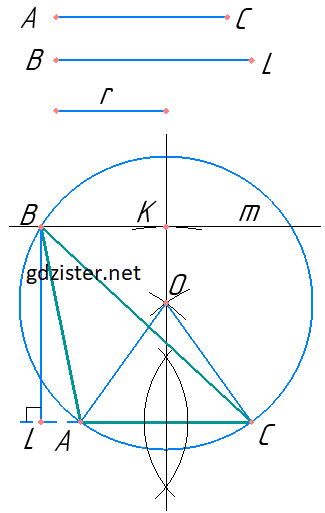
Нехай АС сторона трикутника, BL – висота, проведена до АС, r – радіус описаного кола.
1) Будуємо рівнобедрений ∆OAC за стороною АС та радіусом r;
2) Будуємо коло радіусом r з центром у точці О;
3) Будуємо серединний перпендикуляр відрізка АС;
4) З точки перетину відрізка АС з власним серединним перпендикуляром будуємо дугу рівну BL, яка перетинає його в точці К;
5) будуємо пряму m, що проходить перпендикулярно до серединного перпендикуляра в точці К;
6) пряма m перетинає коло в двох точках. Одну з них позначимо точкою В, яка буде вершиною шуканого трикутника;
7) будуємо BL⊥АС;
8) ∆ABC — шуканий трикутник.
