№ 1306 Алгебра = № 24 ВПТ 11 Математика
Розв'яжіть систему рівнянь трьома способами (графічним, підстановки, додавання):
1) $\begin{cases} x – 2y = 5, \\ x + y = –1; \end{cases}$
2) $\begin{cases} 2x + y = 7,\\ –x + 3y = 0. \end{cases}$
Розв'язок:
1) a) Розв’язування системи рівнянь графічним способом: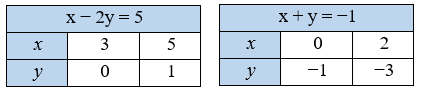
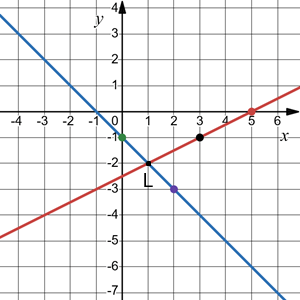
Наближено графіки перетинаються в точці L($\frac{1}{3}$; −$\frac{4}{3}$).
Наближеним розв’язком системи є пара чисел ($\frac{1}{3}$; −$\frac{4}{3}$).
б) розв’язування системи рівнянь методом підстановки:
$\begin{cases} x – 2y = 5, \\ x + y = –1; \end{cases}$ $\begin{cases} x – 2y = 5, \\ x = –1 – y; \end{cases}$
$\begin{cases} –1 – y – 2y = 5, \\ x = –1 – y; \end{cases}$ $\begin{cases} –3y = 6, \\ x = –1 – y; \end{cases}$
$\begin{cases} y = −2, \\ x = 1. \end{cases}$
в) розв’язування системи рівнянь методом додавання:
$\begin{cases} x – 2y = 5 | · (–1), \\ x + y = –1; \end{cases}$
$\begin{cases} –x + 2y = –5, \\ x + y = –1; \end{cases}$ 3y = −6; y = −2.
З другого рівняння першої системи отримаємо:
x − 2 = −1;
x = 1.
2) а) розв’язування системи рівнянь графічним способом: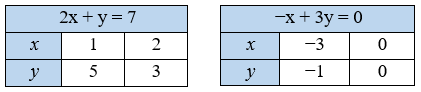
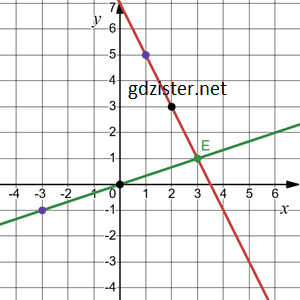
Графіки перетинаються в точці E(3; 1).
Розв’язком системи є пара чисел (3; 1).
б) розв’язування системи рівнянь методом підстановки:
$\begin{cases} 2x + y = 7, \\ –x + 3y = 0; \end{cases}$ $\begin{cases} y = 7 – 2x, \\ –x + 3(7 – 2x) = 0; \end{cases}$
$\begin{cases} y = 7 – 2x, \\ –x + 21 – 6x = 0; \end{cases}$ $\begin{cases} y = 7 – 2x, \\ –7x = –21; \end{cases}$
$\begin{cases} y = 7 – 2x, \\ x = 3; \end{cases}$ $\begin{cases} y = 1, \\ x = 3. \end{cases}$
в) розв’язування системи рівнянь методом додавання:
$\begin{cases} 2x + y = 7, \\ –x + 3y = 0 | · 2; \end{cases}$ $\begin{cases} 2x + y = 7, \\ –2x + 6y = 0; \end{cases}$
7y = 7; y = 1. З першого рівняння першої системи отримаємо:
2x + 1 = 7;
2x = 6;
x = 3.
Відповідь:
1) (1; −2);
2) (3; 1);
