№ 1179 Алгебра = № 54.17 Математика
Розв’яжіть графічно систему рівнянь $\begin{cases} 2x + y = −3, \\ x + 5y = 4. \end{cases}$ Перевірте, чи є одержаний розв’язок точним. Чи є розв’язком даної системи пара чисел (−2$\frac{1}{9}$; 1$\frac{2}{9}$)?
Розв'язок:
Побудую графіки рівнянь на одній координатній площині.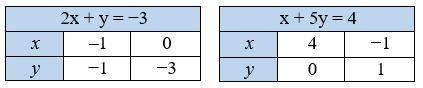
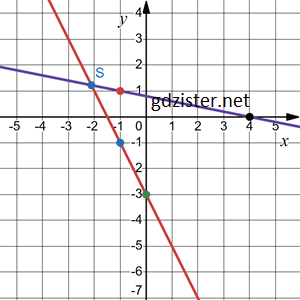
Наближеним розв’язком системи є: x ≈ −2,1; y ≈ 1,2.
$\begin{cases} 2x + y = –3, \\ x + 5y = 4; \end{cases}$
$\begin{cases} 2 · (–2,1) + 1,2 = –3, \\ –2,1 + 5 · 1,2 = 4; \end{cases}$
$\begin{cases} –3 = –3, \\ 3,9 ≠ 4. \end{cases}$
Отже, пара чисел (−2,1; 1,2) не є розв’язком системи.
Пара чисел (−2$\frac{1}{9}$; 1$\frac{2}{9}$) є розв’язком системи
$\begin{cases} 2x + y = –3, \\ x + 5y = 4; \end{cases}$ бо:
$\begin{cases} 2(–\frac{19}{9}) + \frac{11}{9} = –\frac{38}{9} + \frac{11}{9} = –\frac{27}{9} = –3, \\ –\frac{19}{9} + 5\frac{11}{9} = –\frac{19}{9} + \frac{55}{9} = \frac{36}{9}= 4; \end{cases}$
$\begin{cases} –3 = –3, \\ 4 = 4. \end{cases}$
