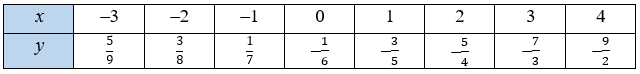№ 1128 Алгебра = № 52.27 Математика
Функцію задано формулою y = $\frac{2x + 1}{x - 6}$. Заповніть у зошиті таблицю, обчисливши відповідні значення функції:

Розв'язок:
y = $\frac{2x +1}{x – 6}$.
Якщо х = –3, то у = $\frac{2 · (–3) + 1}{–3 – 6}$ = $\frac{–6 + 1}{–9}$ = $\frac{5}{9}$.
Якщо х = –2, то у = $\frac{2 · (–2) +1}{–2 – 6}$ = $\frac{–4 + 1}{–8}$ = $\frac{3}{8}$.
Якщо х = –1, то у = $\frac{2 · (–1) +1}{–1 – 6}$ = $\frac{–2 + 1}{–7}$ = $\frac{1}{7}$.
Якщо х = 0, то у = $\frac{2 · 0 + 1}{0 – 6}$ = $\frac{1}{–6}$ = –$\frac{1}{6}$.
Якщо х = 1, то у = $\frac{2 · 1 + 1}{1 – 6}$ = $\frac{3}{–5}$ = –$\frac{3}{5}$.
Якщо х = 2, то у = $\frac{2 · 1 +1}{2 – 6}$ = $\frac{5}{–4}$ = –$\frac{5}{4}$.
Якщо х = 3, то у = $\frac{2 · 3 + 1}{3 – 6}$ = $\frac{7}{–3}$ = –$\frac{7}{3}$.
Якщо х = 4, то у = $\frac{2 · 4 + 1}{4 – 6}$ = $\frac{9}{–2}$ = –$\frac{9}{2}$.