Річна контрольна робота за 7 клас. Варіант 4
(Сторінка 59)
-
Користуючись малюнком, укажіть правильний запис.

А. A ∈ n, B ∉ a
Б. A ∉ n, B ∈ a✅
В. A ∈ n, B ∈ a
Г. A ∉ n, B ∉ a
-
∆KLM — різносторонній, ∆KLM = ∆CDF. Укажіть, якій стороні ∆CDF дорівнює сторона LM.
Розв’язок: у рівних трикутниках всі відповідні елементи рівні (згідно основної властивості рівності трикутників).
А. жодній
Б. CD
В. CF
Г. DF✅
-
Точка О — центр кола, зображеного на малюнку. Укажіть відрізок, що є діаметром кола.
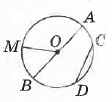
Розв’язок: діаметр кола — це відрізок, що з’єднує дві точки кола і проходить через центр кола.
А. OM
Б. CD
В. AB✅
Г. OA
-
Один з кутів, що утворився при перетині двох прямих, дорівнює 109°. Знайдіть решту кутів та кут між прямими.
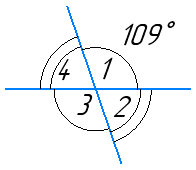
∠2 = 180° – ∠1 = 180° – 109° = 71° (як суміжні)
∠3 = ∠1 = 109° (як вертикальні)
∠4 = ∠2 = 71° (як вертикальні)
Кут між прямими — це найменший із утворених кутів, тобто 71°.
-
Периметр рівнобедреного трикутника 24 см, а його основа — 10 см. Знайдіть бічну сторону трикутника.
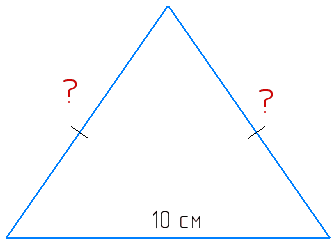
P = 10 + 2 ⋅ x
24 = 10 + 2 ⋅ x
2x = 24 – 10
x = 14 : 2
x = 7 (см)
Відповідь: бічна сторона трикутника 7 см.
- Дано: KB = AL, ∠KBA = ∠LAB. Доведіть, що ∆KBA = ∆LAB.
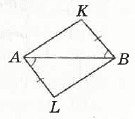
У ∆KBA і ∆LAB:
KB = AL — за умовою;
∠KBA = ∠LAB — за умовою;
AB — спільна сторона.
Отже, ∆KBA = ∆LAB (за 1-ю ознакою рівності трикутників).
- Один з кутів трикутника дорівнює 54°, а другий — на 24° менший за третій. Знайдіть невідомі кути трикутника.
Нехай третій кут — x, тоді другий кут — x – 24°.
Оскільки сума кутів трикутника дорівнює 180°, то:
54° + (x – 24°) + x = 180°
54° + x – 24° + x = 180°
30° + 2x = 180°
2x = 150°
x = 75° — третій кут
x – 24° = 75° – 24° = 51° — другий кут
-
Побудуйте за допомогою циркуля та лінійки без поділок ∆KMP, якщо PM = 5 см, KP = 6 см, ∠P = 80°.
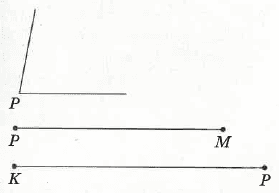
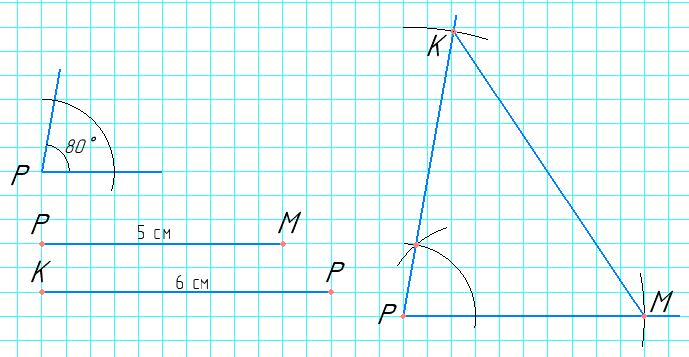
План побудови:
1. Ставимо точку P і від неї проводимо промінь. Розкриваємо циркуль на ширину 5 см і відкладаємо на промені точку M — отримали відрізок PM.
2. Будуємо кут P (80°).
3. Будуємо дугу радіусом 6 см із центром у точці P. На перетині цієї дуги з другим променем кута P отримаємо точку K.
4. З’єднуємо точки K і M. ∆KMP — шуканий.
-
Знайдіть гострі кути прямокутного трикутника, якщо його зовнішні кути при тих самих вершинах відносяться як 17 : 13.
Сума зовнішніх кутів трикутника — 360°
Зовнішній кут при прямому куті — 90°
Другий зовнішній кут = 17x
Третій зовнішній кут = 13x
Складаємо рівняння:
17x + 13x + 90° = 360°
30x = 360° – 90°
30x = 270°
x = 9°
Знаходимо зовнішні кути:
17x = 153°
13x = 117°
Знаходимо гострі кути трикутника:
180° – 153° = 27°
180° – 117° = 63°
