Річна контрольна робота за 7 клас з математики (інтегрований курс). Варіант 4

(Сторінка 63)

1. Користуючись малюнком, укажіть правильний запис.
   
   

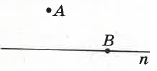
А. A ∈ n, B ∉ n
Б. A ∉ n, B ∈ n✅
В. A ∈ n, B ∈ n
Г. A ∉ n, B ∉ n

2. (a⁶a⁵) : a²  = ...

Розв’язок: (a⁶ ⋅ a⁵) : a² = (a⁶⁺⁵) : a² = a¹¹ : a² = a^11–2 = a⁹

А. a²⁸
Б. a¹⁵
В. a¹⁰
Г. a⁹✅

3. Укажіть точку, що ∉ графіку рівняння x + y = 6.

А. (6; 0)
Б. (6; 1)✅
В. (2; 4)
Г. (4; 2)

4. Спростіть вираз:

1) (c – 6)(c + 6) – c(c – 2) = c² – 36 – c² + 2c = 2c – 36
2) (y + 5)² + (y – 3)(y – 7) = y² + 10y + 25 + y² – 7y – 3y + 21 = 2y² + 46

5. Розкладіть на множники:

1) 6a⁴ + 9a³b = 3a³(2 + 3b)
2) 18m² – 2n² = 2(3m – n)(3m + n)

6. Периметр рівнобедреного трикутника дорівнює 24 см, а його основа — 10 см. Знайдіть бічну сторону трикутника.

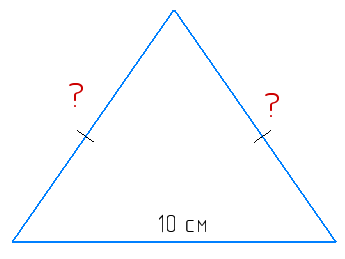
P = 10 + 2 ⋅ x
24 = 10 + 2 ⋅ x
2x = 24 – 10
x = 14 : 2
x = 7 (см)
Відповідь: бічна сторона трикутника 7 см.

7. Один з кутів трикутника дорівнює 54°, а другий — на 24° менший за третій. Знайдіть невідомі кути трикутника.

Нехай третій кут — x, тоді другий кут — x – 24°.
Оскільки сума кутів трикутника дорівнює 180°, то:
54° + (x – 24°) + x = 180°
54° + x – 24° + x = 180°
30° + 2x = 180°
2x = 150°
x = 75° — третій кут
x – 24° = 75° – 24° = 51° — другий кут

8. Розв’яжіть систему рівнянь $\begin{cases}3? + 2? = 4 \\ 4? - 3? = 11\end{cases}$.

Розв’яжемо методом додавання (знищимо одну змінну).
Домножимо обидва рівняння так, щоб коефіцієнти при ? стали однаковими, тобто перше рівняння домножимо на (3), а друге – на (2):
$\begin{cases}9? + 6? = 12 \\ 8? - 6? = 22\end{cases}$
8? + 9? – 6? + 6? = 22 + 12
17? = 34
? = 2

Підставляємо ? = 2 у друге рівняння:
4 ⋅ 2 – 3? = 11
–3? = 3
? = –1

Відповідь: (2; –1).

9. 3 міста М до міста N виїхав велосипедист. Через 2 год з міста N йому назустріч вийшов пішохід. Відстань між містами М і N дорівнює 72 км. Відомо, що швидкість велосипедиста на 8 км/год більша за швидкість пішохода. Знайдіть швидкості велосипедиста і пішохода, якщо до моменту зустрічі пішохід був у дорозі 3 год.

Нехай x — швидкість пішохода, тоді швидкість велосипедиста — x + 8.
Пішохід був у дорозі 3 год, тоді велосипедист — (3 + 2) = 5 год.
Виходить, що пішохід подолав відстань 3х, тоді велосипедист — 5(x + 8).
Разом вони проїхали 72 км. Складемо рівняння:
3x + 5(x + 8) = 72
3x + 5x + 40 = 72
8x = 32
x = 4 (км/год) — швидкість пішохода
x + 8 = 4 + 8 = 12 (км/год) — швидкість велосипедиста