Контрольна робота за ⅠⅠ семестр. Варіант 2

(Сторінка 54-55)

1. Знайдіть другий гострий кут прямокутного трикутника, якщо перший дорівнює 65°.

Розв’язок: у прямокутному трикутнику сума всіх кутів дорівнює 180°, а один з кутів завжди прямий, тобто 90°. Тому сума двох гострих кутів також дорівнює: 180° − 90° = 90°.
Якщо один з гострих кутів дорівнює 65°, то інший гострий кут обчислюється так: 90° − 65° = 25°.

А. 15°
Б. 65°
В. 25°✅
Г. 35°

2. Укажіть малюнок, на якому пряма є дотичною до кола
   

А.
Б.
В.✅
Г.

3. Один із кутів трикутника дорівнює 42°. Знайдіть суму двох інших кутів трикутника.

Розв’язок: сума всіх кутів у будь-якому трикутнику завжди дорівнює 180°.
Якщо один з кутів дорівнює 42°, то сума двох інших кутів буде:
180° − 42° = 138°.

А. Знайти неможливо
Б. 128°
В. 148°
Г. 138°✅

4. AK, BT, CM —  медіани ∆ABC. Яка з них є ще й бісектрисою, і висотою, якщо ∠ A = ∠ С, ∠ А ≠ ∠В.

Розв’язок: якщо ∠A = ∠C, отже, трикутник рівнобедрений, і рівні сторони — це ті, що навпроти рівних кутів, тобто: AB = BC. Тоді вершина трикутника — це B, а основа — AC. У рівнобедреному трикутнику медіана, проведена з вершини до основи, одночасно є і бісектрисою, і висотою. Отже, медіана BT, проведена з вершини B до основи AC, буде медіаною, бісектрисою і висотою.

А. AK
Б. BT✅
В. CM
Г. жодна

5. Зовнішній кут при вершині рівнобедреного трикутника дорівнює 140°. Знайдіть кут при вершині цього трикутника.

Розв’язок: зовнішній і внутрішній кути при вершині — суміжні.
Згідно з теоремою про суміжні кути, їх сума дорівнює 180°.
Отже, внутрішній кут при вершині дорівнює:
180° − 140° = 40°

А. 100°
Б. 40°✅
В. 50°
Г. 110°

6. Радіус кола дорівнює 6 см. Як розміщена пряма а і коло, якщо відстань від центра кола до прямої дорівнює 62 мм.

Розв’язок: оскільки відстань від центра кола до прямої d = 62 мм, більша за радіус кола r = 60 мм, то пряма не має з колом спільних точок.

А. Пряма є дотичною до кола
Б. Пряма перетинає коло в двох точках
В. Пряма не має з колом спільних точок✅
Г. Неможливо визначити

7. На малюнку точка О — центр кола, ∠KOB = 30°. Знайдіть ∠KAB.
   
   

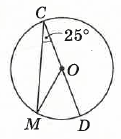
Розв’язок: ∠MCD — вписаний кут, який спирається на дугу MD;
∠MOD — центральний кут, який спирається на ту ж дугу MD, що й вписаний.
Вписаний кут дорівнює половині центрального кута, який спирається на ту саму дугу (згідно теореми про вписаний кут):
∠MCD = ∠MOD : 2
∠MOD = 2 ⋅ ∠MCD
∠MOD = 2 ⋅ 25° = 50°.

А. 75°
Б. 25°
В. 50°✅
Г. 40°

8. Відстані між центрами кіл дорівнює 14 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють 10 см і 6 см.

Розв’язок: обчислимо суму та різницю радіусів
r₁ + r₂ = 10 + 6 = 16 см
∣r₁ − r₂∣ = ∣10 − 6∣ = 4 см
∣r₁​ − r₂​∣ = 4 < d = 14 < 16 = r₁ + r₂​
Оскільки відстань між центрами (d) лежить між різницею і сумою радіусів, кола перетинаються (мають дві спільні точки).

А. Перетинаються✅
Б. Зовнішній дотик
В. Не перетинаються
Г. Внутрішній дотик

9. Зовнішні кути трикутника відносяться як 5 : 6 : 7. Знайдіть більший з внутрішніх кутів трикутника.

Сумарна величина всіх зовнішніх кутів трикутника дорівнює 360°. Позначимо величини зовнішніх кутів як 5?, 6? та 7?.
5? + 6? + 7? = 360°
18? = 360°
? = 20°
Отже, зовнішні кути трикутника дорівнюють:
5? = 5 ⋅ 20° = 100°
6? = 6 ⋅ 20° = 120°
7? = 7 ⋅ 20° = 140°
Внутрішній і зовнішній кути при одній вершині — суміжні, тому:
180° − 100° = 80°
180° − 100° = 60°
180° − 140° = 40°
Таким чином, більший з внутрішніх кутів трикутника дорівнює 80°.

А. 20°
Б. 40°
В. 60°
Г. 80°✅

У завданні 10 установіть відповідність між кутами трикутника KLM та його градусною мірою.

10. У ∆KLM ∠K + ∠L = 130°, ∠L + ∠M = 110°

Кути ∆KLM
1. ∠K
2. ∠L
3. ∠M

Градусні міри
А. 50°
Б. 60°
В. 70°
Г. 80°

Розв’язок:

Запишемо рівняння суми всіх кутів:
∠K + ∠L + ∠M = 180°
Підставимо відомі значення:
∠K + (∠L + ∠M) = 180°
∠K + 110° = 180°
∠K = 180° − 110°
∠K = 70°
Із першого рівняння виразимо:
∠L = 130° − ∠K
∠L = 130° − 70°
∠L = 60°
Із другого рівняння:
∠M = 110° − ∠L
∠M = 110° − 60°
∠M = 50°

Відповідь: 1. В, 2. Б, 3. А.