Контрольна робота за ⅠⅠ семестр. Варіант 1

(Сторінка 52-53)

1. Знайдіть другий гострий кут прямокутного трикутника, якщо перший дорівнює 35°.

Розв’язок: у прямокутному трикутнику сума всіх кутів дорівнює 180°, а один з кутів завжди прямий, тобто 90°. Тому сума двох гострих кутів також дорівнює: 180° − 90° = 90°.
Якщо один з гострих кутів дорівнює 35°, то інший гострий кут обчислюється так: 90° −35° = 55°.

А. 45°
Б. 55°✅
В. 35°
Г. 65°

2. Укажіть малюнок, на якому пряма є січною до кола
   

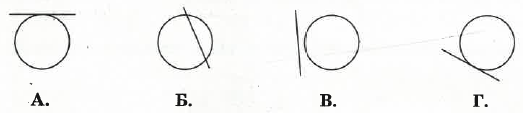
А.
Б.✅
В.
Г.

3. Один із кутів трикутника дорівнює 38°. Знайдіть суму двох інших кутів трикутника.
   

Розв’язок: сума всіх кутів у будь-якому трикутнику завжди дорівнює 180°.
Якщо один з кутів дорівнює 38°, то сума двох інших кутів буде:
180° − 38° = 142°.

А. 132°
Б. 152°
В. 142°✅
Г. знайти неможливо

4. AM, BN, CL —  медіани ∆ABC. Яка з них є ще й бісектрисою, і висотою, якщо ∠B = ∠С, ∠А ≠ ∠В.

Розв’язок: рівність кутів ∠B =∠C означає, що трикутник рівнобедрений з основою AC і рівними сторонами AB = AC. Вершиною рівнобедреного трикутника є А. У рівнобедреному трикутнику медіана, проведена з вершини до основи, одночасно є і бісектрисою, і висотою. Отже, в нашому випадку, AM буде і медіаною, і висотою, і бісектрисою.

А. жодна
Б. AM✅
В. BN
Г. CL

5. Зовнішній кут при вершині рівнобедреного трикутника дорівнює 130°. Знайдіть кут при основі цього трикутника.

Розв’язок: кут при вершині трикутника дорівнює сумі двох внутрішніх протилежних кутів, тобто кутів при основі (згідно теореми про зовнішній кут):
130° = 2х
х = 65°.

А. 55°
Б. 50°
В. 60°
Г. 65°✅

6. Радіус кола дорівнює 5 см. Як розміщена пряма b і коло, якщо відстань від центра кола до прямої дорівнює 48 мм.

Розв’язок: оскільки відстань від центра кола до прямої (d = 48 мм) менша за радіус (r = 5 см = 50 мм), то пряма перетинає коло.

А. Пряма перетинає коло у двох точках✅
Б. Пряма є дотичною до кола
В. Пряма не має з колом спільних точок
Г. Неможливо визначити

7. На малюнку точка О — центр кола, ∠KOB = 30°. Знайдіть ∠KAB.
   
   

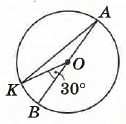
Розв’язок: ∠KOB – центральний кут, ∠KAB – вписаний. Згідно теореми, вписаний кут, що спирається на дугу, дорівнює половині центрального кута, який спирається на ту саму дугу:
∠KAB = ∠KOB : 2 = 30° : 2 = 15°.

А. 45°
Б. 15°✅
В. 30°
Г. 20°

8. Відстані між центрами кіл дорівнює 12 см. Визначте взаємне розміщення цих кіл, якщо їхні радіуси дорівнюють 5 см і 7 см.

Розв’язок: щоб визначити взаємне розміщення двох кіл, порівнюємо відстань між центрами d із:
- Сумою радіусів r₁ + r₂ = 5 + 7 = 12 см
- Різницею радіусів ∣r₁ − r₂∣ = ∣5 − 7∣ = 2 см
Якщо відстань між центрами кіл дорівнює сумі радіусів, то кола зовнішньо дотикаються (мають одну спільну точку ззовні).

А. Перетинаються
Б. Не перетинаюся
В. Внутрішній дотик
Г. Зовнішній дотик✅

9. Зовнішні кути трикутника відносяться як 2 : 3 : 4. Знайдіть менший з внутрішніх кутів трикутника.

Розв’язок: сума всіх зовнішніх кутів трикутника завжди = 360°.
Кути відносяться як 2 : 3 : 4, тому позначаємо їх як 2x, 3x, 4x:
2x + 3x + 4x = 360°
9x = 360°
x = 40°
Знаходимо зовнішні кути:
2x = 2 ⋅ 40° = 80°
3x = 3 ⋅ 40° = 120°
4x = 4 ⋅ 40° = 160°
Внутрішній і зовнішній кути в сумі = 180°, тому внутрішні кути:
180° – 80° = 100°
180° – 120° = 60°
180° – 160° = 20°
Найменший внутрішній кут = 20°

А. 20°✅
Б. 40°
В. 50°
Г. 60°

У завданні 10 установіть відповідність між кутами трикутника ABC та його градусною мірою.

10. У ∆ABC ∠А + ∠В  = 120°, ∠В + ∠С = 130°.

Кути ∆ABC
1. ∠А
2. ∠В
3. ∠С

Градусні міри
А. 40°
Б. 50°
В. 60°
Г. 70°

Розв’язок:
Запишемо рівняння суми всіх кутів:
∠A + ∠B + ∠C = 180°
Підставимо відомі значення:
∠A + (∠B + ∠C) = 180°
∠A + 130° = 180°
∠A = 180° − 130°
∠A = 50°
Із першого заданого рівняння знайдемо:
∠B = 120° − ∠A
∠B = 120° − 50°
∠B = 70°
Із другого рівняння:
∠C = 130° − ∠B
∠C = 130° − 70°
∠C = 60°

Відповідь: 1. Б, 2. Г, 3. В