Контрольна робота за Ⅰ семестр. Варіант 2

(Сторінка 28-29)

1. Кут, градусна міра якого дорівнює 97° є ...

А. прямим
Б. тупим✅
В. розгорнутим
Г. гострим

2. На малюнку прямі c i d перпендикулярні. Укажіть пару, у якій відрізки перпендикулярні.
   

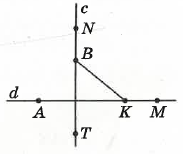
А. AK i NB✅
Б. AK i KB
В. AK i KM
Г. NB i NT

3. Як називаються кути 1 і 2 на малюнку:
   
   

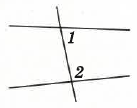
А. Суміжні
Б. Внутрішні різносторонні
В. Відповідні
Г. Внутрішні односторонні✅

4. Знайдіть градусну міру меншого з кутів, які утворилися при перетині двох прямих, якщо сума двох х них дорівнює 300°.

При перетині двох прямих утворюються пари суміжних та вертикальних кутів.

1) 300° : 2 = 150°
2) 180° – 150° = 30°

А. 30°✅
Б. 60°
В. 120°
Г. 150°

5. Точка M лежить між точками C i D, CD = 20 см, CM = $\frac{3}{4}$CD. Знайдіть довжину відрізка MD.
   

MD = CD – CM = CD – $\frac{3}{4}$CD = 20 – $\frac{3}{4}$ × 20 = 20 – 15 = 5 (см).

А. 4 см
Б. 5 см✅
В. 10 см
Г. 15 см

6. На малюнку зображено рівні трикутники. Який із записів правильний?
   

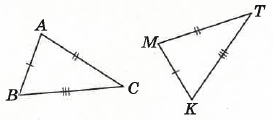
У рівних трикутників відповідні сторони рівні.

А. ∆ABC = ∆TKM
Б. ∆ABC = ∆KMT
В. ∆ABC = ∆MKT✅
Г. ∆ABC = ∆MTK

7. Два суміжних кути відносяться як 4 : 5. Знайдіть міру більшого із цих двох кутів.

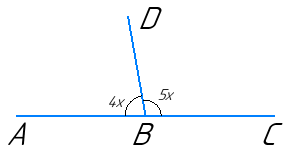
Нехай х – коефіцієнт пропорційності, тоді ∠ABD = 4x, ∠CBD = 5x. Оскільки, суміжні кути в сумі дорівнюють 180° то:

4x + 5х = 180°
9х = 180°
х = 20°

Більший із кутів ∠CBD = 5x = 5 × 20° = 100°

А. 20°
Б. 80°
В. 100°✅
Г. 120°

Г. 108°

8. Один із кутів, що утворилися при перетині двох паралельних прямих січною, дорівнює 118°. Якою із запропонованих може бути градусна міра одного з решти семи кутів?

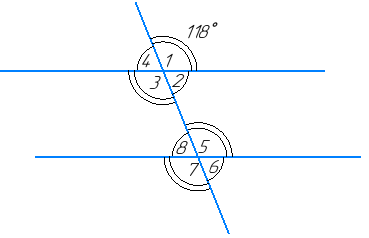
Нехай ∠1 = 118°.
∠1 = ∠3 = 118° (як вертикальні кути).
∠1 = ∠5 = 118° (як відповідні кути).
∠5 = ∠7 = 118° (як вертикальні кути).
∠1 + ∠2 = 180° (як суміжні кути). Звідси
∠2 = 180° – ∠1 = 180° – 118° = 62°.
∠4 = ∠2 = 62° (як вертикальні кути).
∠8 = ∠4 = 62° (як відповідні кути).
∠6 = ∠8 = 62° (як вертикальні кути).
Отже, градусна міра одного з решти семи кутів може бути або 62° або 118°.

А. 59°
Б. 62°✅
В. 72°
Г. 52°

9. Одна із сторін трикутника на 8 см менша від другої й утричі менша від третьої. Знайдіть середню за довжиною сторону трикутника, якщо його периметр дорівнює 33 см.

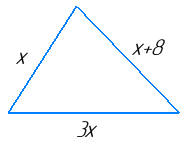
Нехай найменша сторона буде х, тоді друга (х + 8), третя – 3х. Складемо рівняння:

х + х + 8 + 3х = 33
5х + 8 = 33
5х = 25
х = 5 (см) – довжина найменшої сторони
х + 8 = 5 + 8 = 13 (см) – довжина середньої за довжиною сторони
3х = 3 × 5 = 15 (см) – довжина найдовшої сторони.

А. 5 см
Б. 8 см
В. 13 см✅
Г. 15 см

10. ∠COD — розгорнутий, ∠COK = 110°, ∠DOM = 120°.
    

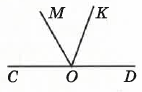
Кут:
1. ∠KOD
2. ∠COM
3. ∠MOK

Градусна міра:
А. 40°
Б. 50°
В. 60°
Г. 70°

∠СOM + ∠MOK + ∠KOВ = 180°
∠СOM = 180° – ∠DOM = 180° – 120° = 60°
∠KOD = 180° – ∠COK = 180° – 110° = 70°
∠MOK = 180° – ∠COM – ∠KOD = 180 – 60° – 70° = 50°

Відповідь: 1. Г, 2. В, 3. Б