ЗПЗ §§ 21–27 Геометрія = ЗПЗ §§ 45-51 Математика
З точки A, що лежить поза колом, проведено до нього дві дотичні AB і AC, де B і C — точки дотику, ∠BAC = 60°. Знайдіть радіус кола, якщо відстань від точки A до центра кола дорівнює 8 см.
Розв'язок:
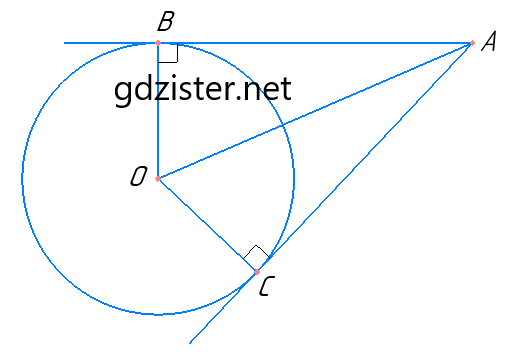
Нехай AB і AC — дотичні (В і С — точки дотику), ∠BAC = 60°, OA = 8 см.
ΔABO = ΔACO (за катетом і гіпотенузою:
OC = OB – як радіуси кола, OA – спільна гіпотенуза).
З рівності трикутників ∠BAO = ∠CAO = $\frac{1}{2}$ ∠BAC = $\frac{1}{2}$ ∙ 60° = 30°.
З прямокутного ΔABO (∠BAO = 30°) маємо: OB = $\frac{1}{2}$OA = $\frac{1}{2}$ ∙ 8 = 4 (см).
Відповідь:
4 см.
