№ 814 Геометрія = № 21 ВПТ 10 Математика
Доведіть, що в рівнобедреному трикутнику центр описаного кола належить прямій, що містить висоту трикутника, проведену до основи.
Розв'язок:
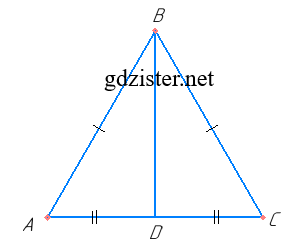
Центр описаного кола лежить на серединних перпендикулярах до сторін трикутника. Нехай ΔABC — рівнобедрений (AB = BC), BD ⊥ AC, тоді AD = DC, оскільки висота, проведена до основи, є медіаною. Маємо BD ⊥ AC і AD = DC, отже, DB належить серединному перпендикуляру до основи AC.
