№ 812 Геометрія = № 19 ВПТ 10 Математика
Вписане в рівнобедрений трикутник коло ділить бічну сторону у відношенні 2:3, починаючи від основи. Знайдіть сторони трикутника, якщо його периметр дорівнює 70 см.
Розв'язок:
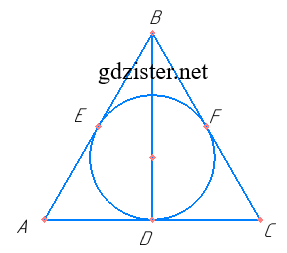
Нехай ΔABC — рівнобедрений (AB = CB), E, F, D – точки дотику.
За умовою EA : EB = 2 : 3. Нехай EA = 2x, EB = 3x.
Враховуючи рівність відрізків дотичних, проведених з однієї точки до кола, маємо:
PΔABC = AB + BC + CA = (2x + 3x) + (3x + 2x) + (2x + 2x) = 14x.
За умовою P = 70 см, отже, 14x = 70 см, x = 5 см.
Тоді AB = BC = 2x + 3x = 5x = 5 ∙ 5 = 25 (см),
AC = 2x + 2x = 4x = 4 ∙ 5 = 20 (см).
Відповідь:
25 см, 25 см, 20 см.
