№ 797 Геометрія = № 4 ВПТ 10 Математика
У колі із центром O проведено діаметр AB і хорди AK і KB. Знайдіть кути трикутника AKB, якщо ∠KOB = 130°.
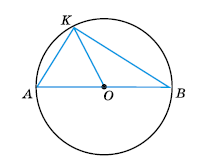
Розв'язок:
∠AOK = зовнішній кут до кута KOB. ∠AOK = 180° – 130° = 50°.
ΔAOK – рівнобедрений, оскільки OA = OK – як радіуси,
тоді ∠OAK = ∠AKO = (180° – 50°) : 2 = 130° : 2 = 65°.
ΔKOB – рівнобедрений, оскільки OK = OB – як радіуси, тоді ∠OKB = ∠OBK = (180° – 130°) : 2 = 25°.
ΔAKB – прямокутний, оскільки діаметр видно з будь – якої точки кола під кутом 90°.
Отже, ∠AKB = 90°. Отже, ∠A = 65°, ∠K = 90°, ∠B = 25°.
Відповідь:
25°, 65°, 90°.
