№ 785 Геометрія = № 51.48 Математика
Побудуйте без транспортира ∆ABC, у якого:
1) AB = 5 см, ∠A = 60°, ∠B = 45°;
2) AB = BC = 4 см, ∠B = 150°.
Розв'язок:
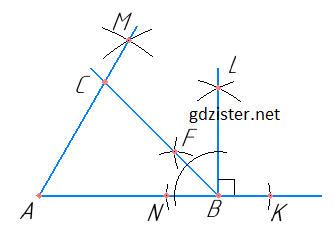
1) 1) Накреслити AB = 5 см;
2) із т. А і т. В радіусом циркуля 5 см опишемо дуги і отримаємо т. М;
3) провести промінь AM; ∠MAB = 60°;
4) продовжити відрізок AB і відкласти від т. В рівні відрізки: NB = BK;
5) з точок N і K провести рівні дуги; з'єднати т. L з т. B; LB ⊥ AB;
6) побудувати бісектрису ∠LBN; ∠NBF = ∠FBL = 45°;
7) продовжити відрізок BF до перетину з AM; т. C — вершина ΔАСВ.
АСВ — шуканий трикутник.
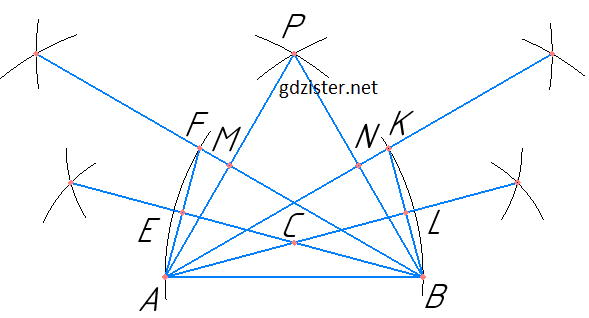
2) Якщо AB = BC, то трикутник рівнобедрений.
∠A = ∠C = (180° – 150°) : 2 = 15°.
1) Побудувати рівносторонній трикутник APB;
2) поділити AP і PB навпіл: AM = MP, PN = NB; ∠NAB = ∠MBA = 30°;
3) відкласти AK = AB і BM = AB, з'єднати т. A і т. М, т. B і т. K;
4) поділити KB і AF навпіл: AE = EM, KL = LB; ∠LAB = ∠EBA = 15°; ∠ACB = 150°.
ACB — шуканий трикутник.