№ 690 Геометрія = № 48.15 Математика
I — точка перетину бісектрис AM і BN рівнобедреного трикутника ABC з основою AB. Доведіть, що IN = IM.
Розв'язок:
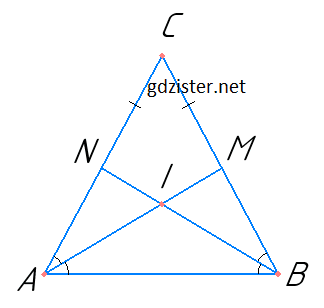
ΔAMB = ΔANB за стороною і двома прилеглими кутами (AB – спільна сторона, ∠A = ∠B – як кути при основі рівнобедреного трикутника, ∠NBA = ∠MAB – як половини рівних кутів).
З рівності трикутників маємо: AN = BM, ∠AMB = ∠ANB.
ΔAIN = ΔBIM за стороною і двома прилеглими кутами (AN = BM – за доведенням, ∠AMB = ∠ANB – за доведенням, ∠NAI = ∠MBI – як половини рівних кутів). З рівності цих трикутників випливає, що IM = IN.
