Завдання № 636

№ 636 Геометрія = № 45.27 Математика

Умова:

Доведіть рівність двох гострокутних рівнобедрених трикутників за основою і висотою, проведеною до бічної сторони.

Розв'язок:

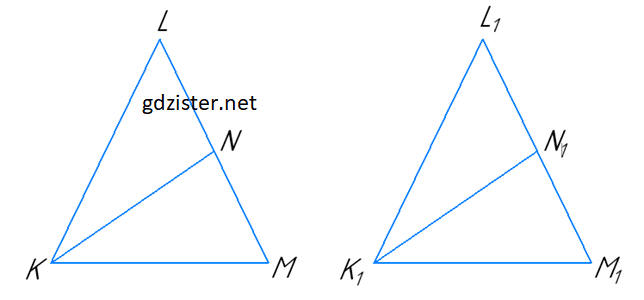
Нехай у рівнобедрених трикутниках KLM і K₁L₁M₁ KL = LM, K₁L₁ = L₁M₁,
KM = K₁M₁, KN ⊥ LM, K₁N₁ ⊥ L₁M₁, KM = K₁M₁. Доведемо, що ΔKLM = ΔK₁L₁M₁.
ΔKNM = ΔK₁N₁M₁ (за гіпотенузою і катетом: KM = K₁M₁, KN = K₁N₁ – за умовою).
З рівності трикутників маємо ∠M = ∠M₁.
∠K = ∠M, ∠K₁ = ∠M₁ – оскільки ΔKLM і ΔK₁L₁M₁ – рівнобедрені. ΔKLM = ΔK₁L₁M₁ за стороною і двома прилеглими кутами
(KM = K₁M₁ – за умовою,∠K = ∠K₁, ∠M = ∠M₁ – за доведенням). 

Відповідь: