: Завдання для перевірки знань до §§11-16 № 1 - 11

Завдання № 9

ЗПЗ §§ 11–16 Геометрія = ЗПЗ §§ 26-31 Математика

Умова:

У рівнобедреному трикутнику KML з основою KL прове дено медіану МР. Знайдіть периметр трикутника KML, якщо МР = 8 дм, а периметр трикутника МКР дорівнює 24 дм.

Розв'язок:

Відповідь до завдання № 9 ЗПЗ §§ 11-16 Геометрія

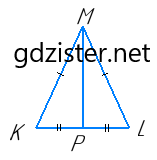
1) MP = 8 дм; P_∆МКР = KM + KP + PM;
P_∆МКР = 24 (дм), тому KM + KP= 24 – 8 = 16 (дм).
2) Оскільки ∆KML — рівнобедрений з основою KL, тo KM = ML.
3) MP – медіана ∆KML, тому KP = PL.
4) P_∆KML = KM + ML + KL = 2KM + 2KP = 2(KM + KP) = 2 ∙ 16 = 32 (дм).

Відповідь:

32 дм.