№ 584 Геометрія = № 9 ВПТ 8 Математика
Умова:
У рівнобедреному трикутнику ABC з основою AB проведено бісектрису AK. Знайдіть:
1) ∠B, якщо ∠AKB = 60°;
2) ∠C, якщо ∠AKC = 111°.
Розв'язок:
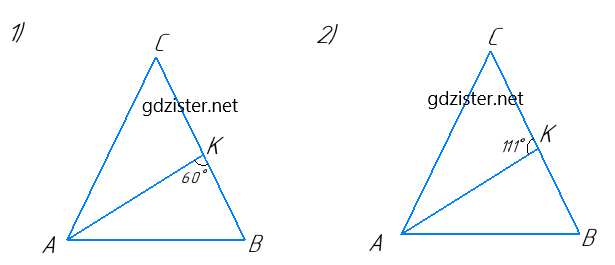
1) Нехай △ABC – рівнобедрений, AC = CB, ∠A = ∠B, AK – бісектриса, ∠AKB = 60°.
Нехай ∠KAB = x, тоді ∠CBA = 2x.
∠KAB + ∠CBA + ∠AKB = 180° (за властивістю суми кутів трикутника).
x + 60° + 2x = 180°;
3x = 120°;
x = 40°.
Отже, ∠KAB = 40°, ∠KBA = 2 · 40° = 80°.
2) Нехай ΔABC – рівнобедрений, AC = AB, ∠A = ∠B.
AK – бісектриса, ∠CAK = ∠KAB, ∠AKC = 111°.
∠AKC + ∠AKB = 180° – як суміжні кути. ∠AKB = 180° – ∠AKC = 180° – 111° = 69°.
Нехай ∠KAB = x, тоді ∠B = 2x.
З ΔAKB: ∠KAB + ∠AKB + ∠KBA = 180°,
x + 69° + 2x = 180°;
3x = 111°;
x = 37°.
Отже, ∠A = ∠B = 37° · 2 = 74°, тоді ∠C = 180° – 2 · 74° = 180° – 148° = 32°.
Відповідь:
1) 80°;
2) 32°.