№ 565 Геометрія = № 22 ВПТ 6 Математика
∆ABC і ∆ABD рівнобедрені зі спільною основою AB. Точки C і D лежать по різні боки від прямої AB. Доведіть, що ∆ACD = ∆BCD.
Розв'язок:
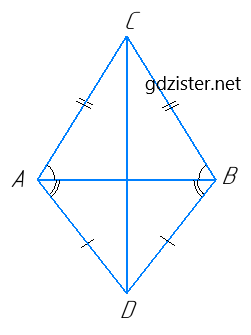
ΔABC — рівнобедрений, AC = CB, тоді ∠CAB = ∠CBA.
ΔABD — рівнобедрений, AD = DB, тоді ∠DAB = ∠DBA.
∠CAD = ∠CAB + ∠DAB, ∠CBD = ∠CBA + ∠DBA, ∠CAD = ∠CBD.
ΔACD = ΔBCD за першою ознакою трикутників
(AC = CB, AD = DB — за умовою, ∠CAD = ∠CBD).
