№ 559 Геометрія = № 16 ВПТ 6 Математика
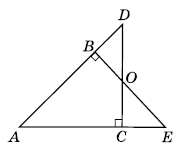
На сторонах кута A позначено точки B і C так, що AB = AC, DC ⊥ AE, BE ⊥ AD. Доведіть, що:
1) BD = CE;
2) AO — бісектриса кута A.
Розв'язок:
1) ∆ABE = ∆ADC за другою ознакою (AB = AC — за умовою, ∠A — спільний, ∠ABE = ∠ADC = 90°, оскільки DC ⊥ AE, BE ⊥ AD). Із рівності трикутників маємо:
AD = AE. Тоді BD = AD - AB, CE = AE – AC.
Оскільки AB = AC за умовою, AD = AE за доведенням, то BD = CE.
2) ∆BOD = ∆COE за стороною і двома прилеглими кутами (BD = CE — за доведеним в п. 1), ∠OBD = ∠OCE = 90°, ∠BDO = ∠CEO — як кути рівних трикутників ACD і ABE. З рівності трикутників маємо BO = CO. ∆ABO = ∆ACO (за двома сторонами і кутом між ними: AB = AC - за умовою, BO = CO — за доведенням, ∠ABO = ∠ACO). Із рівності цих трикутників маємо ∠BAO = ∠CAO, отже, AO — бісектриса кута A.
