ДСР 4 Геометрія = ДСР 8 Математика
У трикутнику два кути дорівнюють 60° і 50°. Знайдіть кут між прямими, що містять бісектриси цих кутів.
A. 125°
Б. 115°
В. 65°
Г. 55°
Розв'язок:
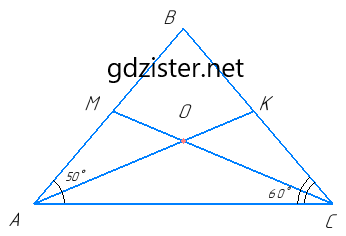
AK — бісектриса ∠A, ∠OAC = ∠BAK = 50° : 2 = 25°.
CM — бісектриса ∠C, ∠MCA = ∠BCM = 60° : 2 = 30°.
З ∆AOC: ∠AOC = 180° - (∠OAC + ∠OCA) = 180° - (25° + 30°) = 125°.
Оскільки кутом між прямими є кут градусною мірою менше ніж 90°, то цим кутом буде кут, суміжний з кутом AOC, який дорівнює 180° - 125° = 55°.
Відповідь:
Г) 55°
