ДСР 4 Геометрія = ДСР 8 Математика
У прямокутному трикутнику один з гострих кутів дорівнює 40°. Установіть відповідність між кутами (1-3) та їхніми градусними мірами (А-Г).
Кути:
1. Кут, що утворює висота трикутника, проведена до гіпотенузи, із більшим катетом.
2. Менший з кутів, що утворює бісектриса прямого кута з гіпотенузою.
3. Кут між прямими, що містять бісектриси прямого і меншого гострого кута трикутника.
Градусні міри:
A. 45°
Б. 50°
В. 65°
Г. 85°
Розв'язок:
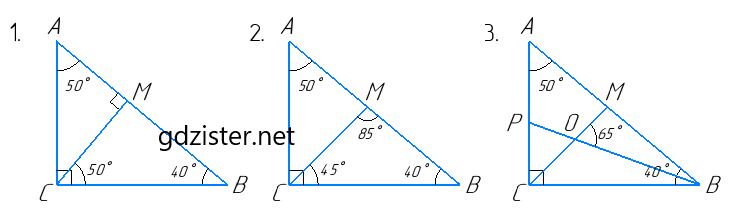
1) Оскільки CM – висота, то ∠CMB = 90°.
Згідно теореми про суму кутів трикутника:
∠MCB = 180° – (∠CMB + ∠MBC) =
= 180° – (90° + 40°) = 50°.
2) Оскільки бісектриса CM ділить ∠С навпіл, то ∠MCB = 45°. Згідно теореми про суму кутів трикутника:
∠CMB = 180° – (∠MCB + ∠MBC) =
= 180° – (45° + 40°) = 85°.
3) ∠РBС = $\frac{1}{2}$ B = $\frac{1}{2}$ × 40° = 20°.
∠MCB = $\frac{1}{2}$ ∠С = $\frac{1}{2}$ × 90° = 45°.
Згідно теореми про суму кутів трикутника:
∠CОB = 180° – (∠ОCB + ∠ОBC) =
= 180° – (45° + 20°) = 115°.
Оскільки кутом між прямими є кут градусною мірою менше ніж 90°, то цим кутом буде кут, суміжний з кутом CОB, який дорівнює 180° - 115° = 65°.
Відповідь:
1) – Б;
2) – Г;
3) – В.
